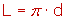HIPÉRBOLA | |
| La hipérbola es una curva abierta y plana, con dos ramas, que se definen como el lugar geométrico de los puntos del plano cuya diferencia de distancias r'-r, a dos puntos fijos F y F', denominados focos, es constante e igual a 2a, siendo 2a la longitud del eje real A-B de la hipérbola. Al ejeCD, se le denomina eje imaginario, siendo su longitud 2b. Ambos ejes se cruzan perpendicularmente en el centro O, punto medio de los dos ejes. Por lo tanto, la hipérbola es simétrica, respecto a los dos ejes. Si, como vemos, la distancia focal F-F' es igual a 2c, se cumplirá que Las rectas que unen un punto cualquiera de la elipse P, con los focos, se denominan radios vectores r y r', y por definición se cumple que r'-r = 2a. Según las dimensiones de los semiejes, se obtendrán tres tipos de parábolas: 1.- Si a > b, se obtendrá una curva de ramas cerradas. 2.- Si a = b, se obtendrá una hipérbola equilátera. 3.- Si a < b, se obtendrá una curva de ramas abiertas. |
PROPIEDADES Y ELEMENTOS
Se denomina circunferencia principal Cp, a la circunferencia de centro O, y diámetro 2a. La circunferencia principal, se define como el lugar geométrico de los pies de las perpendiculares(Q), trazadas desde los focos a las tangentes (t) de la hipérbola. También se puede definir como el punto medio de los segmentos que unen un foco, con la circunferencia focal del otro foco, y las mediatrices de dichos segmentos, son tangentes a la hipérbola.
Se denomina circunferencia focal Cf, a la circunferencia de centro en uno de los focos de la hipérbola, y radio 2a. En una hipérbola se podrán trazar dos circunferencias focales. La circunferencia focal, se define como el lugar geométrico de los puntos simétricos del otro foco (F1), respecto a las tangentes (t) de la hipérbola.
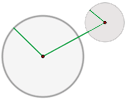
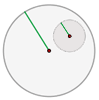
Observando la figura, también podemos definir la hipérbola, como el lugar geométrico de los centros de circunferencia que pasan por un foco, y son tangentes a la circunferencia focal del otro foco.
Se denomina circunferencia focal Cf, a la circunferencia de centro en uno de los focos de la hipérbola, y radio 2a. En una hipérbola se podrán trazar dos circunferencias focales. La circunferencia focal, se define como el lugar geométrico de los puntos simétricos del otro foco (F1), respecto a las tangentes (t) de la hipérbola.
Observando la figura, también podemos definir la hipérbola, como el lugar geométrico de los centros de circunferencia que pasan por un foco, y son tangentes a la circunferencia focal del otro foco.
TRAZADO DE LA HIPÉRBOLA MEDIANTE RADIOS VECTORES
Teniendo en cuenta la definición de la hipérbola, solo necesitaremos coger pares de radios vectores, cuya diferencia sea 2a, para ello determinaremos una serie de puntos sobre el eje real, 1, 2, 3 etc., y cogeremos como parejas de radios vectores, los segmentosA1-B1, A2-B2, A3-B3, y así sucesivamente, determinando los suficientes puntos de la parábola, como para ser definida.
Con cada pareja de radios vectores, se determinarán cuatro puntos de la hipérbola, uno en cada cuadrante de la misma.
Cuanto mayor sea el número de puntos, mayor será la precisión del trazado de la hipérbola, que deberá realizarse, o bien a mano alzada o mediante reglas flexibles, o plantillas de curvas especiales.
Con cada pareja de radios vectores, se determinarán cuatro puntos de la hipérbola, uno en cada cuadrante de la misma.
Cuanto mayor sea el número de puntos, mayor será la precisión del trazado de la hipérbola, que deberá realizarse, o bien a mano alzada o mediante reglas flexibles, o plantillas de curvas especiales.

TRAZADO DE LA HIPÉRBOLA POR HACES PROYECTIVOS
Comenzaremos obteniendo un punto P de la curva por radios vectores, y trazaremos el rectángulo ARPS, y dividiremos los lados RP y PS en un mismo número de partes iguales. Sobre la prolongación de PR y PS llevaremos esas misma divisiones.
Seguidamente trazaremos rectas que unan el vértice A, con las divisiones de PR, y el vértice Br con las divisiones de PS, obteniendo en sus intersecciones, puntos, pertenecientes a la hipérbola buscada. Esto se repetirá para la otra rama de la hipérbola.
Seguidamente trazaremos rectas que unan el vértice A, con las divisiones de PR, y el vértice Br con las divisiones de PS, obteniendo en sus intersecciones, puntos, pertenecientes a la hipérbola buscada. Esto se repetirá para la otra rama de la hipérbola.

TRAZADO DE LA HIPÉRBOLA POR ENVOLVENTES
Esta construcción se basa en el hecho de que la circunferencia principal, es el lugar geométrico de los pies de las perpendiculares trazadas desde el foco a las tangentes a la hipérbola.
Para este trazado partiremos de puntos, de la circunferencia principal. Uniremos dichos puntos con el foco F', y trazaremos por ellos, perpendiculares a las rectas trazadas, obteniendo las rectas tangentes a la parábola. La curva se determinará mediante tangentes a dichas rectas.
Las asíntotas serán las tangentes a la hipérbola en el infinito, y que determinaremos trazando el arco de centro en O y radio O-F. En la intersección de dicho arco con la perpendicular al eje real, trazada por el vértice A, determinaremos el punto 1, perteneciente a la asíntota, solo restará unir dicho punto con el centro O de la hipérbola.
Para este trazado partiremos de puntos, de la circunferencia principal. Uniremos dichos puntos con el foco F', y trazaremos por ellos, perpendiculares a las rectas trazadas, obteniendo las rectas tangentes a la parábola. La curva se determinará mediante tangentes a dichas rectas.
Las asíntotas serán las tangentes a la hipérbola en el infinito, y que determinaremos trazando el arco de centro en O y radio O-F. En la intersección de dicho arco con la perpendicular al eje real, trazada por el vértice A, determinaremos el punto 1, perteneciente a la asíntota, solo restará unir dicho punto con el centro O de la hipérbola.